La procédure pour trouver tous les éléments inconnus d’un triangle avec l’aide d’éléments connus est appelée la "résolution d’un triangle" et la valeur des éléments inconnus est appelée la "solution d’un triangle".
Un triangle est complètement déterminé (tous les éléments sont connus) si 3 des 6 éléments d’un triangle, avec au moins un côté, sont connus.
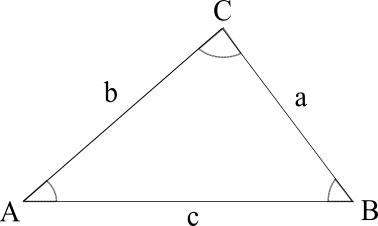
Dans un triangle \(ABC \) quelconque :
- \( A + B + C = \pi = 180°\)
- \( a \lt b+c \ , \ b \lt c+a \ , \ c \lt a + b \). La somme de deux côtés est inférieure au troisième côté.
\( A, B, C\) désignent respectivement les angles \( \widehat{BAC}, \widehat{ABC}, \widehat{ACB} \).
Théorème du sinus
Dans un triangle quelconque \( ABC\),
les sinus des angles sont proportionnels aux côtés opposés :
$$ \dfrac{\sin A}{a} = \dfrac{\sin B}{b} = \dfrac{\sin C}{c} $$
Théorème du cosinus
Dans un triangle quelconque \( ABC\) :
$$\begin{align*}
a^2 = b^2 + c^2 -2bc \cos A & & \Longleftrightarrow & & \cos A = \dfrac{b^2 + c^2 - a^2}{2bc} \\[8pt]
b^2 = a^2 + c^2 -2ac \cos B & & \Longleftrightarrow & & \cos B = \dfrac{a^2 + c^2 - b^2}{2ac} \\[8pt]
c^2 = a^2 + b^2 -2ab \cos C & & \Longleftrightarrow & & \cos C = \dfrac{a^2 + b^2 - c^2}{2ab} \\[8pt]
\end{align*}$$
Théorème de projection
Dans un triangle quelconque \( ABC\) :
$$\begin{align*}
a = b \cos C + c \cos B \\[8pt]
b = a \cos C + c \cos A \\[8pt]
c = a \cos B + b \cos A
\end{align*}$$
Aire d’un triangle
L’aire \( \mathcal {A}\) d’un triangle \( ABC\) est donnée par :
$$\begin{align*}
\mathcal {A} &= \dfrac{1}{2}bc \sin A \\[8pt]
&= \dfrac{1}{2}ca \sin B \\[8pt]
&= \dfrac{1}{2}ab \sin C
\end{align*}$$