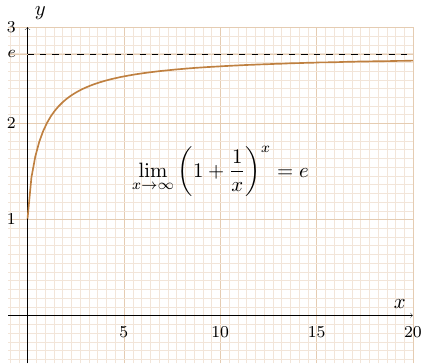Introduction
Lors de la recherche de limites de fonctions, des formes indéterminées peuvent apparaître : \( \dfrac{0}{0}, \dfrac{\infty}{\infty}\).
$$\begin{align*}
\lim_{x \to -1} \dfrac{2x^2-2}{x+1} &&\implies \dfrac{0}{0} \\[8pt]
\lim_{x \to +\infty} \dfrac{3x^2-2}{2x^2+1} &&\implies \dfrac{\infty}{\infty} \\[8pt]
\lim_{x \to 0} \dfrac{e^{2x} -1}{e^x - 1} &&\implies \dfrac{0}{0}
\end{align*}$$
Les formes indéterminées ne garantissent pas qu’une limite existe, ni quelle est cette limite quand elle existe.
On peut s’en sortir souvent avec des pirouettes algébriques:
$$\begin{align*}
\lim_{x \to -1} \dfrac{2x^2-2}{x+1} &= \lim_{x \to -1} \dfrac{2(x+1)(x-1)}{x+1} = \lim_{x \to -1} 2(x-1) = -4 \\[8pt]
\lim_{x \to +\infty} \dfrac{3x^2-2}{2x^2+1} &= \dfrac{3-\dfrac{2}{x^2}}{2 +-\dfrac{1}{x^2} } = \dfrac{3}{2} \\[8pt]
\lim_{x \to 0} \dfrac{e^{2x} -1}{e^x - 1} &= \lim_{x \to 0} \dfrac{(e^x + 1)(e^x - 1)}{e^x - 1} = \lim_{x \to 0} e^x + 1 = 2
\end{align*}$$
Mais toutes les formes indéterminées ne peuvent pas être résolues par des manipulations algébriques, notamment
lorsqu’il s’agit de fonctions transcendantales dans des fonctions algébriques :
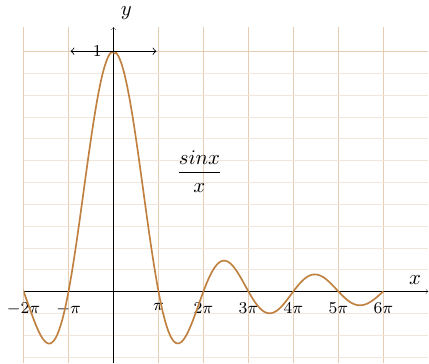
\( \displaystyle { \lim_{x \to 0} \dfrac{\sin x}{x} \implies \dfrac{0}{0} } \)
La règle de L’Hôpital est d’une aide précieuse pour résoudre la plupart des formes indéterminées sous certaines conditions.
Cette règle est une application de la dérivation, mais auparavant il faut voir le théorème des accroissements finis étendus dont elle découle.
Formes indéterminées
Quelles sont les formes indéterminées ?
$$
\begin{array}
{cc|cc}
\textrm{Formes déterminées} & & \textrm{Formes indéterminées} & \\
\hline
\infty + \infty = \infty & -\infty -\infty = -\infty & \infty -\infty =? & \\
\hline
\infty \times \infty = \infty & -\infty \times \infty = -\infty & \dfrac{\infty}{\infty} = ? & \dfrac{-\infty}{-\infty} = ? \\
\infty \times -\infty = -\infty & -\infty \times -\infty = \infty & \dfrac{-\infty}{\infty} = ? & \dfrac{\infty}{-\infty} = ? \\
\hline
& & \dfrac{0}{0} =? & 0 \times \infty =? \\
\hline
0^\infty = 0 & 0^{-\infty} = \infty & 0^0 = ? & \infty^0 = ? \\
& & 1^{\infty} = ? & \\
\end{array}$$
Thèorème des accroissements finis étendu
Le théorème des accroissements finis étendu (aussi appelé deuxième théorème des accroissements finis) est nécessaire pour démontrer la règle de L’Hôpital.
Si f et g sont dérivables sur un intervalle \( ]a,b[ \) et continues sur \( [a,b] \)
telles que \( g'(x) \ne 0 \) pour tout \( x \in [a,b] \), alors il existe un point \( c \in ]a,b[ \) pour lequel :
$$
\dfrac{f'(c)}{g'(c)} = \dfrac{f(b) - f(a)}{g(b) -g(a)}
$$
Règle de L’Hôpital
Soient f et g deux fonctions dérivables sur un intervalle ouvert \( ]a,b[ \)
contenant \( c \), sauf éventuellement en \( c \).
Supposons que \( g'(x) \ne 0 \) pour tout \( x \in [a,b] \), sauf éventuellement en \( c \).
Si la limite de \( \dfrac{f(x)}{g(x)} \) quand \( x \) approche \( c \) est une forme indéterminée \( 0/0 \), alors :
$$ \lim_{x \to c} \dfrac{f(x)}{g(x)} = \lim_{x \to c} \dfrac{f'(x)}{g'(x)} $$
pourvu que la limite à droite existe (ou soit infinie).
Ce théorème couvre également les cas où la limite de \( \dfrac{f(x)}{g(x)} \) quand \( x \) approche \( c \) aboutit aux
formes indéterminées \( +\infty / +\infty\), \( -\infty / +\infty\), \( +\infty / -\infty\), \( -\infty / -\infty\).
La règle de L’Hôpital s’applique aussi sur les limites à droite, à gauche.
$$ \lim_{x \to c^+} \dfrac{f(x)}{g(x)} = \lim_{x \to c^+} \dfrac{f'(x)}{g'(x)} $$
La forme doit être indéterminée, si la limite existe, la règle ne s’applique pas !
Pour s’en convaincre, un très simple exemple :
$$\begin{align*} f(x) &= 2x^2 & g(x) &= x \\[8pt]
f'(x) &= 4x & g'(x) &= 1 \\[14pt]
\lim_{x \to 1} \dfrac{f(x)}{g(x)} &= 2 & \lim_{x \to 1} \dfrac{f'(x)}{g'(x)} &= 4
\end{align*}$$
\( \displaystyle { \lim_{x \to 0} \dfrac{e^{2x} - 1}{x} } \)
La forme est indéterminée : \(0 / 0 \). Application de la règle de L’Hôpital.
$$
\lim_{x \to 0} \dfrac{e^{2x} - 1}{x} = \lim_{x \to 0} \dfrac{ \dfrac{d(e^{2x} - 1)}{dx} }{ \dfrac{d(x)}{dx} }
= \lim_{x \to 0} \dfrac{ 2e^{2x} }{ 1 }
= 2
$$
\( \displaystyle { \lim_{x \to \infty} \dfrac{\ln x}{x} } \)
La forme est indéterminée : \(\infty / \infty \). Application de la règle de L’Hôpital.
$$
\lim_{x \to \infty} \dfrac{\ln x}{x} = \lim_{x \to \infty} \dfrac{ \dfrac{d(\ln x)}{dx} }{ \dfrac{d(x)}{dx} }
= \lim_{x \to \infty} \dfrac{ 1 }{ x } =0
$$
Applications en cascade
Parfois, il est nécessaire d’appliquer la règle de L’Hôpital plus d’une fois :
\( \displaystyle { \lim_{x \to -\infty} \dfrac{x^2}{e^{-x}} } \)
La forme est indéterminée \( +\infty / +\infty\). Application de la règle de L’Hôpital.
$$
\lim_{x \to -\infty} \dfrac{x^2}{e^{-x}} = \lim_{x \to -\infty} \dfrac{ \dfrac{ d(x^2) }{ dx } }{ \dfrac{ d(e^{-x}) }{ dx } }
= \lim_{x \to -\infty} \dfrac{ 2x }{ - e^{-x} }
$$ Cette limite est également une forme indéterminée : \( -\infty / +\infty \). Réapplication de la règle de L’Hôpital.
$$
\lim_{x \to -\infty} \dfrac{2x}{- e^{-x}} = \lim_{x \to -\infty} \dfrac{ \dfrac{ d(2x) }{ dx } }{ \dfrac{ d(- e^{-x}) }{ dx } }
= \lim_{x \to -\infty} \dfrac{ 2 }{ e^{-x} }
= 0
$$
Autres formes indéterminées
La règle de L’Hôpital ne couvre pas les autres formes indéterminées, formes qui ne déterminent pas la valeur de la limite,
ni même si elle existe :
$$\begin{align*} 0 \times \infty && 1^{\infty} && \infty^0 && 0^0 && \infty - \infty \end{align*}$$
Réécriture de l’expression
Pour les formes \(0 \times \infty\) et \(\infty - \infty\), essayer de réécrire l’expression pour faire apparaître les formes \(0/0\) ou \(\infty/\infty\) et ainsi pouvoir appliquer la règle de L’Hôpital.
\( \displaystyle { \lim_{x \to \infty} e^{-x}\sqrt{x} \implies 0 \times \infty ,\ \textrm{réécriture} } \)
$$\begin{align*}
\lim_{x \to \infty} e^{-x}\sqrt{x} &= \lim_{x \to \infty} \dfrac{\sqrt{x}}{e^x} && \implies \dfrac{0}{0}, \ \textrm{ Règle de L’Hôpital } \\[8pt]
&= \lim_{x \to \infty} \dfrac{ \dfrac{d(\sqrt{x})}{dx} }{ \dfrac{d(e^x)}{dx} }
= \lim_{x \to \infty} \dfrac{ 1 }{ 2\sqrt{x} \ e^x } = 0
\end{align*}$$
\( \displaystyle { \lim_{x \to 1^+} \left( \dfrac{1}{\ln x} - \dfrac{1}{x-1} \right) \implies \infty - \infty}, \ \textrm{réécriture} \)
$$\begin{align*}
\lim_{x \to 1^+} \left( \dfrac{1}{\ln x} - \dfrac{1}{x-1} \right)
&= \lim_{x \to 1^+} \dfrac{x - 1 - \ln x}{(x-1)\ln x} && \implies \dfrac{0}{0}, \ \textrm{Règle de L’Hôpital} \\[8pt]
&= \lim_{x \to 1^+} \dfrac{ \dfrac{d(x - 1 - \ln x)}{dx} }{ \dfrac{ d ((x-1)\ln x)} {dx} } \\[8pt]
&= \lim_{x \to 1^+} \dfrac{ 1 - \dfrac{1}{x} }{ \ln x + (x-1)\dfrac{ 1} {x} } \\[8pt]
&= \lim_{x \to 1^+} \dfrac{ x - 1 }{ x \ln x + x - 1 } && \implies \dfrac{0}{0}, \ \textrm{Règle de L’Hôpital} \\[8pt]
&= \lim_{x \to 1^+} \dfrac{ \dfrac{d(x - 1)}{dx} }{ \dfrac{d(x \ln x + x - 1)}{dx} } \\[8pt]
&= \lim_{x \to 1^+} \dfrac{ 1 }{ 1 + \ln x + 1 } = \dfrac{ 1 }{ 2 }
\end{align*}$$
Formes indéterminées avec exposants
Les formes \(1^{\infty}\), \(\infty^0\) et \(0^0\) découlent de fonctions qui ont des bases et exposants variables.
Dans ce type de fonctions, utiliser les logarithmes (même procédure que la dérivation logarithmique).
\( \displaystyle { \lim_{x \to \infty} \left( 1 + \dfrac{1}{x} \right)^x \implies 1^{\infty} } \)
On pose \( y = \displaystyle { \lim_{x \to \infty} \left( 1 + \dfrac{1}{x} \right)^x }\)
$$\begin{align*}
\ln y = \ln \left( \lim_{x \to \infty} \left( 1 + \dfrac{1}{x} \right)^x \right) &= \lim_{x \to \infty} \ln \left(1 + \dfrac{1}{x} \right)^x \\[8pt]
&= \lim_{x \to \infty} x \ln \left( 1 + \dfrac{1}{x} \right) && \implies 0 \times \infty , \ \textrm{ Forme indéterminée, réécriture } \\[8pt]
&= \lim_{x \to \infty} \dfrac{\left( 1 + \dfrac{1}{x} \right) }{ \dfrac{1}{x} } && \implies 0/0, \ \textrm{ Règle de L’Hôpital } \\[8pt]
&= \lim_{x \to \infty} \dfrac{ \dfrac{d \left( 1 + \dfrac{1}{x} \right) } {dx} }{ \dfrac{d \left(\dfrac{1}{x} \right)}{dx} }
= \lim_{x \to \infty} \dfrac{-\dfrac{1}{x^2} }{ -\dfrac{1}{x^2} } = 1
\end{align*}
$$\(\ln y = 1 \implies y = e \)
\( \displaystyle { \lim_{x \to \infty} \left( 1 + \dfrac{1}{x} \right)^x } = e \)
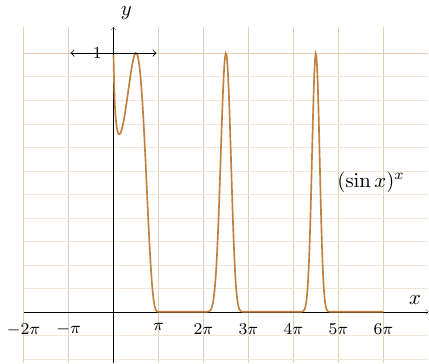
\( \displaystyle { \lim_{x \to 0^+} (\sin x)^x \implies 0^{0} } \)
On pose \(\displaystyle { y = \lim_{x \to 0^+} (\sin x)^x }\)
$$\begin{align*}
\ln y = \ln \lim_{x \to 0^+} (\sin x)^x &= \lim_{x \to 0^+} \ln (\sin x )^x \\[8pt]
&= \lim_{x \to 0^+} x \ln (\sin x ) && \implies 0 \times -\infty, \ \textrm{réécriture} \\[8pt]
&= \lim_{x \to 0^+} \dfrac{\ln (\sin x )}{\dfrac{1}{x}} && \implies \dfrac{-\infty}{+\infty}, \ \textrm{Règle de L’Hôpital} \\[8pt]
&= \lim_{x \to 0^+} \dfrac{ \dfrac{d(\ln (\sin x ))}{dx}} {\dfrac{d \dfrac{1}{x}}{dx} }
= \lim_{x \to 0^+} \dfrac{ \dfrac{\cos x}{\sin x}} {-\dfrac{1}{x^2}} = \lim_{x \to 0^+} \dfrac{ -x^2 } { \tan x} && \implies \dfrac{0}{0}, \ \textrm{Règle de L’Hôpital} \\[8pt]
&= \lim_{x \to 0^+} - \dfrac{ \dfrac{d(x^2)}{dx}} {\dfrac{d(\tan x)}{dx} } = \lim_{x \to 0^+} - \dfrac{ 2x } { \sec^2 x} = 0
\end{align*}
$$\(\ln y = 0 \implies y=1\)
\( \displaystyle { \lim_{x \to 0^+} (\sin x)^x = 1 } \)
Exercices et problèmes